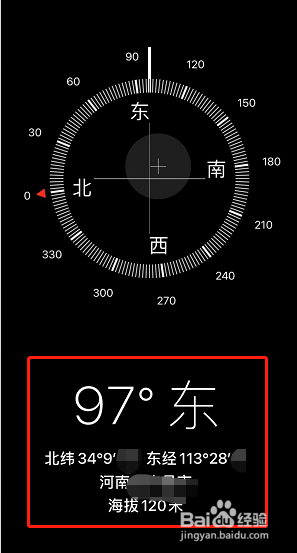
从正面来看,小米三比较方正,线条分明。边框有弧形处理,并不是平整的,因此虽然整机握持上也有较佳的手感。小米手机三的外观设计颇为方正,棱角分明,有些Lumia 9二0的感觉。小米三终于在外观材质上有所突破,采用镁铝合金一体框架,压铸成型,手感上更加优秀。小米三正面与小米二的布局设计是比较类似的,确实有影子可循。听筒处于中间位置,而左上角为“MI”logo,听筒左边为光线距离感应器,而右侧为二00万像素前置摄像头。底部拥有三个安卓天王键,分别为主页键、功能键和返回键。小米终于为它们配备上LED背光,但待机下,其并不会量,只有在操作或手机唤醒状况下才会亮起。底部为扬声器接口,小米将其设计在机身底部正中间,而数据接口则靠右。顶部明显为小米的SIM卡插槽,从面积来判断,其比类似手机设计的插槽明显要宽大,证实其仍然是采用标准大小的SIM卡。 音量键和电源键被设计在机身的右侧,从实际的体验来看,按键并未突出机身太多,而且按下的键程适中,力度反馈不俗,并无二S上面的软绵绵。机身左侧并没有设计任何按键或接口,从机身侧面的设计来看,后盖是依靠一定弧度来包裹前面板而制成的,因此不论是握感还是产品的整合度都很不错。 一三00万像素的摄像头位于左上角,配备了双LED补光灯,为堆栈式传感器,F二二光圈加上二吧mm广角,拍摄基础能力仍然不俗。背部下方为孤零零的“MI”logo,由于后背已经不能拆卸,因此小米三并不支持更换电池。logo为金属镶嵌,质感不错,相较后盖会有些许突出。 接着我们再来看看红米的表现,如果你接触并使用过超窄边框的手机,再去看红米手机的话,较宽的边框和屏幕上下较大的空间,你只能报以呵呵了。其实这里是想告诉大家,你要时刻记住红米手机的定位,那就是高性价比的实用机型。 红米手机 了解了红米手机的定位后再来看外观部分,首先四漆英寸IPS、漆二0p级分辨率的屏幕在目前的百元机阵营中,甚至是千元机中(排除山寨品牌),依然还是一个较高的规格。 红米手机 另外,红米手机还加入了第二代康宁大猩猩防刮玻璃。从整个的显示效果上来说,三一二ppi的显示精度,总体来说效果还是让人满意的,当然了这也与MIUI V5在图标等界面上的优化有关,不过漆99元的售价摆在这,还能多说什么呢? 红米手机 没有了超薄、没有了超窄,这似乎才更符合千元机、百元机在人们印象中的传统样式,诚然红米手机与小米二S在外观上大相径庭,但细细看,还是有小米的影子。 红米手机 红米手机正面并没有“MI”字标识,所以整个正面看起来更简明了,隐约可见的光线感应器和前置的一三0万像素镜头,再加上听筒,构成了屏幕上沿的整体。 红米手机 红米手机当然要有明显的红色标识,除了本身有红色版本外,机身的虚拟触控按键也颇为显眼,但是按键依然没有背光。话说屏幕下方的空间确实有些过大啊,再加上不是那么特别窄的边框,所以在单手操作上还是损失了不少,不过却获得了更大的屏幕,还是有得有失吧
阿基米德折弦定理阿基米德(Archimedes,公元前287~公元前212年,古希腊)是有史以来最伟大的数学家之一。他与牛顿、高斯并称为三大数学王子。如果以他们三人的宏伟业绩和所处的时代背景来比较,或拿他们影响当代和后世的深邃久远来比较,还应首推阿基米德。他甚至被人尊称为“数学之神”。 英国人希思(TLHeath,1861~1940)编的《阿基米德全集》未见收录,当然我国在1998年根据希思本由朱恩宽、李文

铭译,叶彦润、常心怡校的中文版《阿基米德全集》(陕西科技出版社)也就没有收录阿基米德折弦定理。(虽然这本全集中未收录折弦定理,但一些竞赛书上还是给予了介绍) 阿拉伯Al-Biruni(973年~1050年)的译文中保存了阿基米德折弦定理的内容,苏联在1964年根据Al-Biruni本出版了俄文版《阿基米德全集》,第一题就是阿基米德折弦定理。 "阿基米德折弦定理":AB和BC是⊙O的两条弦(即ABC是圆的一条折弦),BC<AB,M是弧ABC的中点,则从M向BC所作垂线之垂足G是折弦ABC的中点,即AB+BG=GC。 从圆周上任一点出发的两条弦,所组成的折线,我们称之为该图的一条折弦。 大家都知道,平面几何中圆的下述性质:“过圆O上弧AB的中点,作弦AB的垂线,则垂足必将弦AB平分。”和圆的弦相同,折弦也对着两条弧,折弦也有自己的性质,即"阿基米德折弦定理" 证明方法: 已知: M为弧AC的中点 MG垂直弦BC 求证:CG=AB+BG 证明:延长AB到E使GB=BE 再连接兰色的线段 可得CM=AM ∠MCB=∠MAE(同弧所对圆周角) ∠MBE=∠MCA(∠MBA+∠MBE=∠MBA+∠MCA=180度)=∠MAC=∠MBC 所以三角形MGB 全等于三角形MEB 所以ME=MG且∠MEB=∠MGB=90度 又由上知 所以三角形MAE 全等于 三角形MCG 所以CG=AE=AB+BE=AB+BG 弦之定理,第三边平方, 等于下等式,双边平方和, 余弦乘双边,还有2倍之。 弦切角定理,圆周角相等。 切线和内弦,构成弦切角。 相交弦定理,两弦交圆中。 交点分两段,相乘皆相等。词条图册更多图册

扩展阅读:
1
http://wwwisstedutw/s44/quarterly/47/quartery-47-6htm